[Tech report] How I analyzed 337,576 financial statements

Some fun math and a bit of right-wing politics.

This post is for those who like Machine Learning and Math. The next post will be about business/finance so feel free to skip this one! Or else, just jump to the “What about politics” section.

When I had the idea of completing the financial statements analysis, I genuinely believed it would take no more than 8 hours. I ended up spending over 40.

Data acquisition

Everything begins with data. I got in touch with Financial Modeling Prep to see if they could grant me a full, free access to their API in exchange for a bit of promotion. They agreed.

Downloading the data was quite straightforward. The only challenge was dumping JSON objects larger than 1GB. To avoid overloading the RAM of my old laptop, I split the data into multiple files. In total, I obtained financial reports from 25,866 companies, with up to 30 years of historical data each.

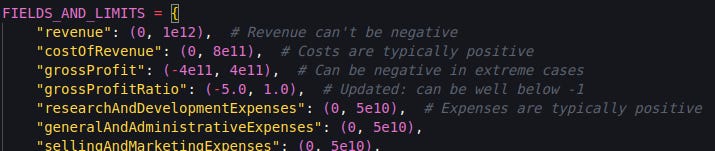
It's important to note that a value of 0 for a line item can have multiple meanings. It could indicate that the line item is not applicable to the specific financial statement (e.g., Cost of Revenue or Inventory for a Bank). Alternatively, it might mean the data scraper at Financial Modeling Prep was unable to locate the data, or it could truly represent a value of 0. So, a 0 in the data does not necessarily signify a value between -0.1 and 0.1, but rather signifies one of the following: a non-applicable item, a value that was not found, or an actual value of 0.

Data cleaning

Data cleaning proved to be more difficult than anticipated. I initially assumed the data would be clean. But when I realized that the average Revenue in my whole dataset was 1e28 dollars and the average net profit margin was 5000% (net income 50 times higher than revenue on average) I suspected that maybe something was wrong. So I asked Claude to come up with upper and lower bounds for each of the report lines. After a few back and forth passes, it gave me sensible limits.

By the way, since a good portion of the statements were reported in a currency other than the USD, I had to convert the numbers before applying the limits. And as some of the line items were ratios, I had to exclude them from the exchange-rate conversion process.

I tried two different approaches about what to do with invalid statements:

• Discarding the statement and all other reports from the same company

• Replacing the invalid value with an arbitrary value, such as 0.01, unlikely to exist elsewhere in the dataset. (Remember this value, as I will refer to it later.)

The first one resulted in over 80% of the statements being discarded, which made the dataset too small: my model was immediately overfitting and the val loss was terrible.

The second one resulted in a very sparse dataset. On average, approximately 40% of the inputs were either zeros (ie not applicable, such as Cost of Revenue in bank’s statements) or 0.01 (ie invalid data).

Which is not ideal, because these are false zeros. They don’t carry the same information as a real value of 0. They are qualitatively different from “something small, between -0.1 and 0.1”, and they should be treated accordingly.

On the one hand, I want my model to be quite linear because my problem is also largely linear, and I don't want the model to be so complex that it's prone to overfitting. On the other hand, 40% of my values need to be treated in a completely non-linear fashion. There needs to be a clear distinction between a 0 (not applicable), a 0.01 (invalid data, which should be disregarded), and a 0.02 (a normal, genuine near-zero value). This behavior is not typical for MLPs, as it's inherently non-linear. Hence, a slightly fancier architecture can be useful.

Now, you can’t just feed a model with raw financial data: having some inputs with mean and sd below 1 (like ratios) alongside Revenue figures in the billions is far from best practice. So one of the best things you can do is normalize the data so that mean = 0 and sd = 1, for all input features. For example, if the average revenue across the whole dataset is 1 billion, and its standard deviation is also about 1 billion, we should convert each revenue value using the formula:

\(normalized\_revenue = \frac{revenue - 10⁹}{10⁹}\)

Or, more generally:

\(normalized\_value = \frac{value - mean}{standard\_deviation}\)

Let’s imagine we exclude the original invalid values from normalization. That’s to say we normalize everything except for 0 and 0.01, that we keep as they are. By doing this, we are effectively ensuring that these unknown or not-applicable values are treated as average values. Indeed, 0 is now the exact average (by construction) of our new value distribution, and 0.01 is close to that average, being just 0.01 standard deviations above it. This approach is beneficial as it aligns with the natural heuristic: "If I don't know the exact figure, I assume it's not too far from average," which we humans use when guess-timating.

Now that we have made everything possible on the dataset side to mitigate the problems caused by these strange values, let’s see how architecture comes into play.

Over engineering a NN architecture: the ultimate guide

Here are the general features of the model:

• Input dim: 101 features/year * 3 years = 303 features

• Output dim: 8 features for next year ¹.

• Training data:

  • inputs: financial statements for years n-3, n-2 and n-1 (every possible one until last_year-2)

  • outputs: 8 features from year n’s financial statement (until last_year-1)

• Val data:

  • inputs: financial statements for last_year-3, last_year-2 and last_year-1

  • outputs: 8 features from last year’s financial statements

I can hear people thinking “there is massive data leakage, beginner’s mistake, haha”. I kindly suggest the people thinking that should have their kneecaps split (link is safe, no worries).

If you're curious about that concern, please refer to the Appendix section. For now, let's move on to the network's architecture.

Network architecture choice

When predicting sequence data, RNNs and Transformers are often considered the go-to models. In our case, they would be unsuitable.
As we saw in the previous post, a persistence model is very effective and it doesn’t get more linear than that. When a simple linear regression does an acceptable job, there is usually no need for a fancier architecture than a simple MLP.

As explained in the Data cleaning section, the values 0 and 0.01 should ideally be treated differently from typical near-zero numbers. So I tried to design an architecture that allows for that without departing too much from a standard FFN².

I first had an idea that was quite mathematically sound but turned out to be a parameter-inefficient, hardly convergent, overfitting-prone mess³.

Then, a second approach, simpler and quite similar to the former one from a mathematical standpoint, avoided matrix computations. It proved to be a partial failure: it was slightly less parameter efficient than a simple MLP, while being better at handling very sparse data⁴.

Finally, a third approach worked perfectly. It achieved a lower test loss while using less parameters than a MLP and resulted in cleaner gradients which were easier to interpret.

The basic, non-optimized version is incredibly simple.

First, for each input vector (a flat vector with 303 features – 101 for each year over 3 years), a `mask_invalid` vector is created. This is a 303-dimensional vector where each position has a 1 if the corresponding value in the input vector is 0.01 (the code for 'off-bounds'), and a 0 otherwise.
It’s really a kind of grid that, overlaid on the original input vector, would show where the invalid values are.

Next, a `mask_zero` vector is defined in the same way. This vector indicates the positions of the 0 values in the input vector.

Then, these three vectors are concatenated and given to a simple Linear layer + LeakyReLU. The first third of the output vector is considered the next layer’s input_vector, and the other two thirds are the mask_invalid and mask_zero vectors. It’s equivalent to a simple MLP which input_vector is
concat(values_input_vector, mask_invalid, mask_zero) and output is a 8-dimensional prediction vector.

So this un-optimized network consisted of two Masked Layers (it’s the name I used for them) and a linear output layer.

If we look at the parameter count of one Masked Layer, we have:

\(N = (3 \cdot input\_size) \cdot (3 \cdot output\_size) + 3 \cdot output\_size\)

The term before the “+” refers to the size of the transformation matrix and the term after refers to the bias of our layer.

This is quite a lot. Of course, it’s easily handled by my laptop, but let’s remember that parameter count directly influences overfitting proneness on small datasets (like ours). The more parameters a model has, the more it will be able to learn the noise of the training dataset and struggle with test loss.

Moreover, we can definitely sense that such an architecture is not optimal. Two thirds of the concatenated input vector are very light on information (a mere 303*2 = 606 bits, compared to 303*32 = 9,696 bits for the first third⁵) and two-thirds of the matrix’s parameters are wasted just to handle this small amount of information.

The first thing that could be done to decrease the number of parameters is to project each of the input_values and masks into a smaller sub-space before concatenating them.

At first I tried projecting them into different sub-spaces through different projection matrices, and it yielded good results.

Then I tried using the same projection matrix for all three projections, on the very scientific ground of “Hell yeah, I bet it works” and you bet it worked fine, achieving even lower test loss (while increasing train loss), which is perfect.

So the general architecture of one layer looked like that:

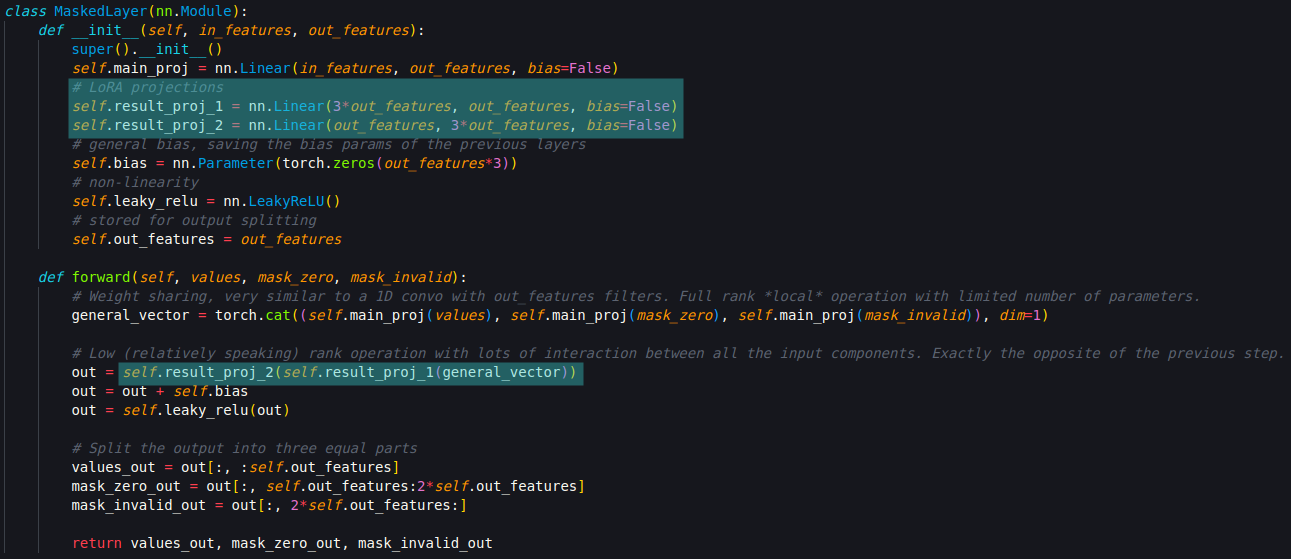
I then computed the condition number of each matrix and got quite a high number (~1e3) for each layer’s result_proj matrix. It was a clear indication that I could LoRA⁶ them. I did so with a compression ratio of 3.

Then we have the final architecture of our layers, that looks like the following:

All in all, the model has 24,625 parameters and achieves 3.5% better test loss compared to the best MLP I came up with, that has 49,459 parameters.

Of Convos and LoRAs: why this architecture works so well.

The first part of the forward pass is equivalent to a 1D convolution with out_features filters, in_features stride and filter_size + flattening with interleaving each filter’s result.

What this means is that the projection matrix main_proj gets optimized to select filters that maximize information retained from each of the input vector’s 3 parts. Just like a normal learned projection matrix does, you may say, but the difference is that it has to make concessions to find the best filters for all three sub parts. This is analogous to a CNN learning the best filters for processing images.

And in our case, it works fine: the similarity in data presentation means that a single filter is likely to effectively process both the main values and their corresponding masks.

The contrast between the two stages of the forward pass is particularly interesting. The first stage achieves parameter efficiency through weight-sharing and convolutions, while the second achieves it by LoRA-ing the transformation matrix.

Here is why it works:

• Convolutions aim to find the (usually) full-rank down projection that best captures local features across the image, using a fixed number of parameters. The only global interaction between features in convolutions comes from the competition to change the filters' weights during back-propagation.

• LoRAs are about finding the down projection that best captures global features/interaction, and expanding the result in a meaningful way. It results in a low-rank transformation.

Basically, the convolution finds a common ground for features interaction, and the LoRA projection enforces this interaction, all in a parameter efficient manner.

Training

Here is a comparison between the best MLP and the best Masked Net (the above mentioned architecture) I could design.

We can see that there is likely some room for improvement in weight initialization. Furthermore, the training loss is higher for the masked network compared to the MLP, while the validation loss is lower. This suggests reduced risk of overfitting and better predictive potential.

Conclusion/Executive summary

• Data Preprocessing Matters. Careful data cleaning and normalization, including separate handling of invalid data and genuine zeros, was critical.

• Masked Nets perform great. Link to github repo is in the comments section if you need to use them.

• Parameter efficiency is key. A parameter-inefficient net is not only compute intensive to train, but also at risk of overfitting on small datasets.

Appendix

Data leakage concerns

Let’s focus on a single company. During training, the model will be presented with data from say, 2009, 2010, 2011 and asked to predict the 8 desired features for year 2012. It will also see, either before or after the aforementioned training example (training examples are randomly presented) another one that looks like 2008, 2009, 2010, and asked about 2011. At such point the model could think “Haha, I know what I have to predict because I have seen the data sometime before in my inputs”. So it will just parrot back the 2011 report as “stored” in its weights. The model is just learning to parrot things back, not to predict them.

The problem is especially noticeable in the case of transformers. If you don’t mask the upper part of the attention matrix, the transformer will be able to peek into future tokens and output them without trying to predict them⁷. Even if you properly mask it, presenting a transformer with overlapping sequences will favor such behavior: it will learn sequences rather than language rules.

So this concern is theoretically valid. But it doesn’t mean that ML zealots have the right to live.

Why it isn’t a big deal.

Three reasons:

• In order to learn sequences, a model must have a lot of “storage space”, meaning a lot of parameters relative to the size of the training dataset. Which is not the case for our ~24k parameters model, trained on a 130MB dataset.

• Models prone to data leakage are those whose behavior is very non-linear, such as transformers and RNNs. Our prediction model is quite linear, using only two low-dimensional LeakyReLU layers, which is nowhere near the 3rd degree polynomial attention seen in transformers (not even accounting for the softmax).

• Predicting financial statements is fundamentally linear. One of the best naive prediction model is just a persistence model (ie predicting the numbers will stay the same as before): an identity matrix with no bias, it doesn’t get more linear than that.
  So it’s unreasonable to think that the Adam optimizer will tune weights to encourage sequence memorizing while both the data and the network’s architecture favor a quasi-linear behavior. ML fanatics should be piledrived (link is safe).

A real world, political analogy

Let’s imagine three people who need to talk to smooth over some minor disagreement.
The first is a heavy weight boxer with a fair sized chip on his shoulder.
The second one is a non-violent communicator who holds little grudge against the two others because he has learned to process his bad negative painful feelings.
The third is a social justice warrior, full of indignation against the world, including the other two.
One of their common friends, who’s called Convolution (a name he didn't choose), tries to find the best place for all of them to “talk”. The boxer immediately calls for a box ring. The non-violent guy wants to talk through the disagreement in a nice, calm place and suggests the others should come over at his place. The SJW doesn’t want to talk at all (sorry guys I tried to keep the post non political until now but it’s impossible due to the deeply controversial nature of the topic).
Convolution then says, 'Well, SJW doesn't want to communicate; the Non-Violent one wants a calm place but doesn't hold a grudge, so his opinion doesn't matter as much, and the Boxer wants a ring, so we'll go with the ring.
Convolution just found the best place for each of the three to talk.

I skip the part where Non-Violent submits a kind and empathetic disagreement to Convolution on that matter and SJW calls out the systemic violence of the capitalist system that oppresses the weak. They all meet at the local gym, on the box ring.

At first, Non-Violent and SJW are a bit hesitant and cling to the ropes. Then the referee, whose name is LoRA Down Projection (obviously didn’t choose either) pulls them off the ropes and shoves them into a smaller space with Boxer. He then says “I want the disagreement settled in ten minutes”. Boxer needs less time to explain with loads of compassion that he was hurt by the two others and that he’s happy to have a thoughtful conversation to figure out what went wrong. And you know, he likes to talk with his hands.
Seven minutes later, they all come to the common conclusion that everything is fine, it’s never been finer, boxer, “you’re my best friend we’re brothers in arms forever (but please release mine, I want to use them again some time)”. A lawyer passing by, whose name is LoRA Up (you bet) decides to translate this informal agreement into legal terms. So, he expands the “everything’s fine” conclusion to 35 pages and sends them to the judge.

Blah blah ever after.

1. ["revenue", "netIncome", "eps", "epsdiluted", "freeCashFlow", "totalStockholdersEquity", "operatingCashFlow", "dividendsPaid"]

2. FFN (feed forward network) and MLP (multi-layer perceptron) can be used interchangeably as they basically mean the same thing: linear layers with non-linearity between.

3. It was about interpolating missing values using a regression matrix (that basically said “Here is my best guess for metric X based on the other 302 metrics”, like “Oh, the Revenue line is missing but I will be able to infer it from COGS, Operating expenses and EBITDA”), with each “guess” weight-averaged by a Softmaxed learned covariance-like matrix, parameterized by the mask of missing/invalid values. Mathematically speaking, it was the “soundest” architecture, but it had too many parameters, involved complex matrix computations and was an absolute mess to train. I couldn’t use LayerNorms because they messed with the regression nature of the task. This architecture was an utter failure. It didn’t converge most of the time and when it did, there were obvious signs of overfitting.

4. Before going through the main neural net, every missing metric in the input was inferred from the others using a simple Linear layer, the result was multiplied by a mask vector (1 where data is missing/invalid, 0 otherwise), then added to the main input vector, resulting in a full input vector with each 0 replaced by a nice inferred value. This architecture kind of worked: replacing Linear layers by these “masked interpolation layers” resulted in a net improvement, but it was less parameter-efficient than a MLP due to a much higher parameter count in each layer. It was a partial failure, but I used this architecture for my previous post, out of pride to use MY architecture instead of a basic one.

5. This is just an estimate, as the “real” information stored in the vectors is also dependent on their data distribution and the architecture they are fed into.

6. Here, LoRA is the acronym for Low Rank Approximation and not Low Rank Adaptation.

7. You can check my french posts on how ChatGPT works. Maybe I’ll translate them but it might be hard as the examples I used don’t work in English.